A Rancher Has 400 Feet of Fencing

Find the dimensions that maximize the enclosed area. The equation for the area of a rectangle is.

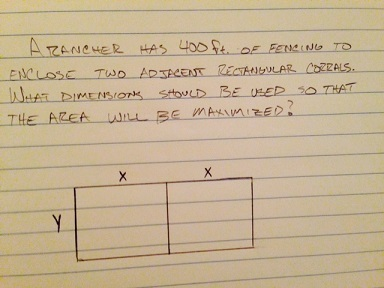
Solved A Rancher Has 400 Ft Of Fencing To Enclose Two Chegg Com

So thats why the access are close to each other here and got the sides for like the other.

. A rancher has 400 feet of fencing to put around a rectangular field and then subdivide the field into 3 identical smaller rectangular plots by placing two fences parallel to. B What dimensions produce a maximum enclosed area. LLDATUDY DUPPURD Question 10 of 17 Step 1 of 1 1225 Correct A rancher has 400 feet of fencing to put around a rectangular field and then subdivide the field into 3 identical smaller rectangular plots by placing two fences parallel to one of the fields shorter sides.

Find the dimensions that maximize the enclosed area. Preview 400 3 4 3 Preview. What dimensions should be used so that the enclosed area wil.

A rancher has 400 feet of fencing to enclose two adjacent rectangular. Find the dimensions that maximize the enclosed area. My Notes Ask Your Teacher A manufacturer of lighting fixtures has daily production.

Transcribed Image TextA rancher has 400 feet of fencing to enclose two adjacent rectangular corrals see figure. Perimeter 6x4x 400. So the corresponding area will be the maximum area that is equal to 500 by three.

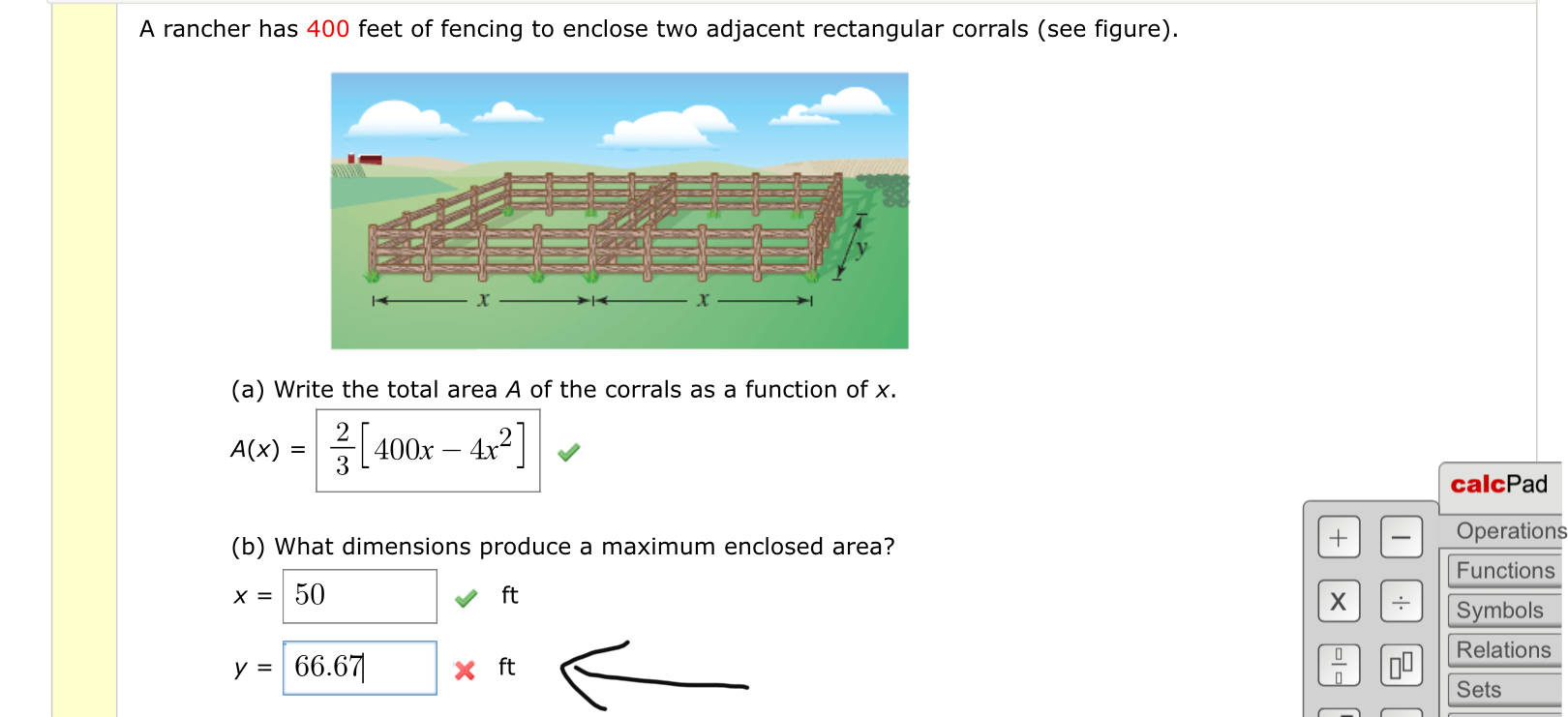
A rancher has 400 feet of fencing to enclose two adjacent rectangular corrals see figure. What dimensions should be used so that the enclosed area will be a maximum. Problem 22 Easy Difficulty A rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals see figure.

200 2 x 200-2x 200 2 x. One of the fields shorter sides. Write your answers as fractions reduced to lowest terms.

Area 3 40² 34040 4800 sqft. X ft y ft Expert Solution. If the dimensions are w and l the total perimeter of the two rectangular corrals is 4w4l but with a common side this is equal to 4w 3l.

Or 10x 400. A rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals. Answers 2 So for this optimization problem were given that we have two adjacent frank tackles.

Write rectangular plots by placing fence parallel to your answers as fractions reduced to lowest terms Answer Keypad We dont have your requested question but here is a. Therefore the second length of sides are. A rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals.

Accordingly it has 6 Lengths and 4 Widths. A rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals see figure. Write your answers as fractions reduced to lowest terms.

About 500 Of Fencing A Has Feet Rancher A rancher has 400 feet of fencing to enclose two adjacent rectangular corrals. A Express the area of the field as a function of the length 1. Length of rectangle is x.

Write your answers as fractions reduced to. Ax b What dimensions produce a maximum enclosed area. Or x 40010.

Now the enclosed area is. Length red FIELD width w RIVER No fencing this side on. If rancher wants to build a corral into three equal rectangles.

Watch More Solved Questions in Chapter 3 Problem 1 Problem 2. Find the dimensions that maximize the enclosed area. Next step here is were going to derive respect to X both sides equation and what we have here its 200 over to minus six X squared sorry six X over to is equal to zero.

Write your answers as fractions reduced to lowest terms. What dimensions should be used so that the enclosed area will be a maximum. Write your answers as fractions reduced to lowest terms.

What dimensions should be used so that the enclosed area will be a maximum. A Write the total area A of the corrals as a function of x. Let three corrals are in the form of square of Side x feet.

A rancher has 400 feet of fencing to put around a rectangular field and then subdivide the field into 2 identical smaller rectangular plots by placing a fence parallel to one of the fields shorter sides. Or x 40 feet. A rancher has 400 feet of fencing to enclose two adjacent rectangular corrals as shown in the following figure.

A rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals. For the remaining two sides we know that they are equal in length but not their dimensions in relation to the first pair. A rancher has 400 feet of fencing with which to enclose two adjacent rectangular corrals see figure.

He will use 400 feet of fencing and doesnt plan to fence the side along the riverbank see the picture below for reference. The cost to build a closet averages 2013 with a. A rancher has 400 feet of fencing to put around a rectangular field and then subdivide the field into 2 identical smaller rectangular plots by placing a fence parallel to one of the fields shorter sides.

Well it seems that Ive become stuck with a couple of these wonderful homework problems and I sure could use some helpful advicehintssolutions. Answer x 50 y 200 3 View Answer Discussion You must be signed in to discuss. Nov 14 2005.

What dimensions should be used so that the enclosed area will be a maximum. B Find the average rate of change of the area as the length goes from 100 to 200 feet. Therefore maximum area of three rectangular square is 4800 ft².

Multiplying out here weve got 200 x minus three X squared all over to sequel to the max. Simple thing out here. A x y Axy A x y.

A rancher has 600 feet of- fencing to put around one of the fields shorter sides Find rectangular field and then subdivide the field into 2 identical smaller the dimensions that maximize the enclosed area. A rancher has 400 feet of fencing to close tho adjacent rectangular corrals see figure. For this shape we know.

-1 points LarColAlg10 31069. A rancher has 600 feet of fencing to put around a rectangular field and then subdivide the field into 3 identical smaller rectangular plots by placing two fences parallel to one of the fields shorter sides. Find the dimensions that maximize the enclosed area.

The equation describing the enclosed area is 400 A2 23 كل من 4 T 3 400 4 20 3 3 т 2 To enclose the maximum area what should be the dimensions of each corral. A Write the total area of the corrals as a function of x.

Solved A Rancher Has 400 Feet Of Fencing To Enclose Two Chegg Com

Solved A Rancher Has 400 Feet Of Fencing With Which To Chegg Com

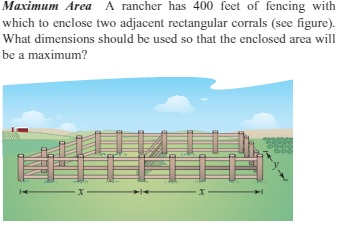
Solved A Rancher Has 400 Feet Of Fencing With Which To Chegg Com